단의 개발 블로그
소수 찾기 본문
💡 문제
1부터 입력받은 숫자 n 사이에 있는 소수의 개수를 반환하는 함수, solution을 만들어 보세요.
소수는 1과 자기 자신으로만 나누어지는 수를 의미합니다.
(1은 소수가 아닙니다.)
💡 제한 조건
- n은 2이상 1000000이하의 자연수입니다.
입출력 예
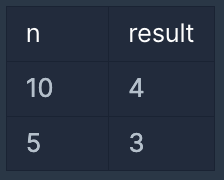
입출력 예 설명
입출력 예 #1
1부터 10 사이의 소수는 [2,3,5,7] 4개가 존재하므로 4를 반환
입출력 예 #2
1부터 5 사이의 소수는 [2,3,5] 3개가 존재하므로 3를 반환
✨ 풀이
class Solution {
public int solution(int n) {
int answer = 0;
for(int i=1; i<= n; i++) {
if(i==1) continue;
if(isPrime(i)) answer++;
}
return answer;
}
boolean isPrime(int n) {
for(int i = 2; i <=Math.sqrt(n); i++) {
if(n % i == 0) return false;
}
return true;
}
}1. 1은 소수가 아니므로 제외한다.
2. 단순히 자기 자신과 i 값을 비교하며 나머지 값만 체크하면 시간초과 오류가 발생한다.
3. 소수는 결국 자기와 대칭되는 값이 존재하므로 제곱근을 사용하여 계산하면 더 좋은 수행시간을 갖게된다.
다른 방법으로는 에라토스테네스의 체가 있다. 간단히 설명하면, 판별한 소수 값의 배수를 모두 지워가며 소수를 구하는 방법이다. 각 문제의 요구사항에 맞게 편한것을 사용하면 되는데, 만약 더 짧은 수행시간을 요구하면 해당 알고리즘을 사용하여 문제를 해결해야 한다. 아래는 에라토스테네스의 체를 사용한 코드이다.
class Solution {
public int solution(int n) {
int answer = 0;
boolean[] prime = new boolean[n+1];
for(int i=2; i<=n; i++){
prime[i] = true;
}
for(int i=2; i<=Math.sqrt(n); i++) {
if(prime[i]) {
for(int j=i+i; j<=n; j+=i) {
prime[j] = false;
}
}
}
for(boolean p : prime) {
if(p) answer++;
}
return answer;
}
}
왼쪽이 제곱근, 오른쪽이 에라토스테네스의 체 사용한 결과이다.


'Algorithm > JAVA' 카테고리의 다른 글
| 성격 유형 검사하기 (0) | 2024.11.02 |
|---|---|
| 숫자 짝궁 (0) | 2024.11.02 |
| [1차] 다트게임 (1) | 2024.11.01 |
| 로또의 최고 순위와 최저 순위 (0) | 2024.10.31 |
| 실패율 (0) | 2024.10.30 |




